Formula Specification in Templates

The list of formula specifications used in Templates. (Notes: bold inputs for functions are linked to the data in program).

Logical

Name	Syntax, parameters	Description	Example
AND	AND(Boolean1;Boolean2; ... )	Returns TRUE if all of its arguments are TRUE	AND(3=3;2=2) ⇒ TRUE
OR	OR(Boolean1;Boolean2; ... )	Returns TRUE if any of its arguments are TRUE	OR(3=4;2=3) ⇒ FALSE
TRUE	TRUE()	Returns the logical value TRUE	IF(TRUE();1;2) ⇒ 1
FALSE	FALSE()	Returns the logical value FALSE	IF(FALSE();1;2) ⇒ 2
IF	IF(Test;Then;Else)	Specifies a logical test to perform - inputs can be linked to data - result can be number, text, logical value	Result is number (bold inputs linked to data X[0;1;2;3;4;5;6]): IF(220>200;220-200;200-220) ⇒ 20 IF(120>MAX([X⇕]);120;-1) ⇒ 120 IF(MAX([X⇓2:⇓3])>[X⇓7];MAX([X⇓2:⇓3]);[X⇓7])) ⇒ 6 IF(MAX(⟨1;2⟩)>6;MAX(⟨1;2⟩);6) ⇒ 6 Result is text: Input [Coordinate Z] = 210;[GWT] = 180 IF([Coordinate Z]>0;"Above terrain";"Under terrain") ⇒ "Top above terrain" IF([GWT]<[Coordinate Z];"GWT under top of the test.";"Measure error.") ⇒ "GWT under top of the test."
IFS	IFS(Test1;Then1;Test2;Then2; ... ;Else)	Checks whether one or more conditions are met and returns a value that corresponds to the first TRUE condition	Input [GWT] = 15 IFS([GWT]>8;10;[GWT]>6;9;[GWT]>3;8;-1) ⇒ 10
NOT	NOT(Boolean)	Reverses the logic of its argument	IF(NOT(5>6);175;155) ⇒ 175 IF(NOT(5>4);175;155) ⇒ 155 IF(NOT("A"="B");175;155)⇒ 175
SWITCH	SWITCH(Switch;Case1;Result1;Case2;Result2; ... ;[ Else ])	Evaluates an expression against a list of values and returns the result corresponding to the first matching value. If there is no match, an optional default value may be returned	SWITCH(50>6;TRUE();44;FALSE();56;-111) ⇒ 44 SWITCH(30/6;3;120;4;220;5;320;420) ⇒ 320

Mathematical

Name	Syntax, parameters	Description	Example
ABS	ABS(Number)	Returns the absolute value of a number	ABS(120) ⇒ 120; ABS(-120) ⇒ 120
ACOS	ACOS(Number)	Returns the arccosine of a number ⟨-Pi/2; Pi/2⟩	for Number=0.5 ... DEGREES(ACOS(0.5)) ⇒ 60°
ACOT	ACOT(Number)	Returns the arccotangent of a number ⟨0; Pi⟩	for Number=1 ... DEGREES(ACOT(1)) ⇒ 45°
ASIN	ASIN(Number)	Returns the arcsine of a number ⟨-Pi/2; Pi/2⟩	for Number=0.5 ... DEGREES(ASIN(0.5)) ⇒ 30°
ATAN	ATAN(Number)	Returns the arctangent of a number ⟨-Pi/2; Pi/2⟩	for Number=1 ... DEGREES(ATAN(1)) ⇒ 45°
CEILING	CEILING(Number;[Multiple=1];[Mode=0])	Rounds a number to the nearest integer or to the nearest multiple of significance - if Number<0 and Mode<>0 ⇒ result is rounded up - if Number<0 and Mode=0 ⇒ result is rounded down	CEILING(10.4) ⇒ 11 CEILING(10.4;1) ⇒ 11 CEILING(10.4;5) ⇒ 15 CEILING(10.8;5) ⇒ 15 CEILING(-10.4;5;0) ⇒ -10 CEILING(-10.4;5;1) ⇒ -15 CEILING(-10.4;2;0) ⇒ -10 CEILING(-10.4;2;1) ⇒ -12
COS	COS(Angle[rad])	Returns the cosine of the given angle in rad	for α=60° ... COS(RADIANS(60)) ⇒ 0.5
SIN	SIN(Angle[rad])	Returns the sine of the given angle in rad	for α=30° ... SIN(RADIANS(30)) ⇒ 0.5
COT	COT(Angle[rad])	Returns the cotangent of an angle in rad	for α=45° ... COT(RADIANS(45)) ⇒ 1
TAN	TAN(Angle[rad])	Returns the tangent of an angle in rad	for α=45° ... TAN(RADIANS(45)) ⇒ 1
EXP	EXP(Number)	Returns e raised to the power of a given number	EXP(1) ⇒ 2.71828
FLOOR	FLOOR(Number;[Multiple=1];[Mode=0])	Rounds a number down, to the nearest integer multiple of significance - if Number<0 and Mode<>0 ⇒ result is rounded to zero - if Number<0 and Mode=0 ⇒ result is rounded away from zero	FLOOR(10.4;1;0) ⇒ 10 FLOOR(10.9;1;0) ⇒ 10 FLOOR(10.4;7;0) ⇒ 7 FLOOR(-10.4;1;0) ⇒ -11 FLOOR(-10.4;1;1) ⇒ -10 FLOOR(-10.4;7;0) ⇒ -14 FLOOR(-10.4;7;1) ⇒ -7
LN	LN(Number)	Returns the natural logarithm of a number	LN(1)) ⇒ 0; LN(EXP(1)) ⇒ 1
LOG	LOG(Number;[Base=10])	Returns the logarithm of a number to a specified base (10 if missing)	LOG(1; 10) ⇒ 0; LOG(10; 10) ⇒ 1
LOG10	LOG10(Number)	Returns the base-10 logarithm of a number	LOG10(1) ⇒ 0; LOG10(10) ⇒ 1
MROUND	MROUND(Number;Multiple)	Returns a number rounded to the desired multiple - rounds up, if the remainder after dividing the number by the multiple is ≥ to Multiple / 2.	MROUND(10.4;1) ⇒ 10 MROUND(10.4;2) ⇒ 10 MROUND(10;3) ⇒ 9 (Remainder = 1 < 1.5 (Multiple/2) MROUND(11;3) ⇒ 12 (Remainder = 2 > 1.5 (Multiple/2)
PI	PI()	Returns the value of pi	PI() ⇒ 3.141592653
POWER	POWER(Base;Number)	Returns the result of a number raised to a power	POWER(2;4) ⇒ 16
SQR	SQR(Number)	Returns the result of a squared number	SQR(5) ⇒ 25; SQR(-5) ⇒ 25
SQRT	SQRT(Number)	Returns a positive square root of a positive Number	SQRT(36) ⇒ 6; SQRT(-36) ⇒ NAN
SUM	SUM(Number1;Number2; ... )	Returns the sum of a series of numbers	Inputs linked to data X[0;1;2;3;4;5;6]): SUM([X⇓2:⇓5]) ... SUM(⟨1; 2; 3; 4⟩) ⇒ 10 SUM([X⇕]) ⇒ 21
DEG	DEGREES(Angle [rad])	Converts radians into degrees	DEGREES(PI()) ⇒ 180°; DEGREES(PI()/2) ⇒ 90°
RADIANS	RADIANS(Number)	Converts degrees to radians	RADIANS(180) ⇒ π (3.141592653)
ROUND	ROUND(Number;Places)	Rounds a number to a specified number of digits - negative Places round to the left of the decimal point	ROUND(58.563;3) ⇒ 58.563 ROUND(58.563;2) ⇒ 58.56 ROUND(58.563;1) ⇒ 58.6 ROUND(58.563;0) ⇒ 59 ROUND(58.563;-1) ⇒ 60 ROUND(58.563;-2) ⇒ 100
ROUNDUP	ROUNDUP(Number;Places)	Rounds a number up, toward zero	ROUNDUP(58.563;3) ⇒ 58.564 ROUNDUP(58.563;2) ⇒ 58.57 ROUNDUP(58.563;1) ⇒ 58.6 ROUNDUP(58.563;0) ⇒ 59
ROUNDDOWN	ROUNDDOWN(Number;Places)	Rounds a number down, toward zero	ROUNDDOWN(58.563;3) ⇒ 58.563 ROUNDDOWN(58.563;2) ⇒ 58.56 ROUNDDOWN(58.563;1) ⇒ 58.5 ROUNDDOWN(58.563;0) ⇒ 58 ROUNDDOWN(58.563;-1) ⇒ 50 ROUNDDOWN(58.563;-2) ⇒ 0

Text

Name	Syntax, parameters	Description	Example
CONCAT	CONCAT(Value1;Value2; ... )	Combines the text from multiple ranges and/or strings, but it doesn't provide the delimiter or IgnoreEmpty arguments - Value1, Value2, ... can be as Text or Number	CONCAT(12;34;56) ⇒ 123456.000 CONCAT("12";"34";"56") ⇒ 123456.000 CONCAT(12;"34";56) ⇒ 123456.000 Input [GWTb] = 15 CONCAT([GWTb];" m") ⇒ "15 m"
LEFT	LEFT(Text;[Count=1])	Returns the leftmost characters from a text value	LEFT("qwert";3) ⇒ "qwe" LEFT("qwert";1) ⇒ "q"
RIGHT	RIGHT(Text;[Count=1])	Returns the rightmost characters from a text value	RIGHT("qwert";3) ⇒ "ert" RIGHT("qwert";1) ⇒ "t"
LEN	LEN(Text)	Returns the number of characters in a text string	LEN("qwert") ⇒ 5 LEN("") ⇒ 0
SEARCH	SEARCH(Find text;Within text;[Start=1])	Finds one text value within another (not case-sensitive)	SEARCH("G";"Hello GEO!";1) ⇒ 7

Statistical

Name	Syntax, parameters	Description	Example
AVERAGE	AVERAGE(Number1;Number2; ... )	Returns the average of its arguments	AVERAGE(3;5;1) ⇒ 3 Inputs linked to data X[0;1;2;3;4;5;6]): AVERAGE([X⇓3:⇓5]) ... AVERAGE(⟨2; 3; 4⟩) ⇒ 3
MAX	MAX(Number1;Number2; ... )	Returns the maximum value in a list of arguments	MAX(3;5;1) ⇒ 5 Inputs linked to data X[0;1;2;3;4;5;6]): MAX([X⇓3:⇓5]) ... AVERAGE(⟨2; 3; 4⟩) ⇒ 3
MIN	MIN(Number1;Number2; ... )	Returns the minimum value in a list of arguments	MIN(3;5;1) ⇒ 1 Inputs linked to data X[0;1;2;3;4;5;6]): MIN([X⇓3:⇓5]) ... AVERAGE(⟨2; 3; 4⟩) ⇒ 2
PERCENTIL	PERCENTILE(Array;k)	Returns the k-th percentile of values in a range	Inputs linked to data X[1;2;3;4;5]): PERCENTILE([X⇕];0.5) ⇒ 3
PERCENTILE.EXC	PERCENTILE.EXC(Array;k)	Returns the k-th percentile of values in a range, where k is in the range 0..1, exclusive	Inputs linked to data X[1;2;3;4;5]): PERCENTILE.INC([X⇕];1) ⇒ NAN PERCENTILE.INC([X⇕];0.4) ⇒ 2.4
PERCENTILE.INC	PERCENTILE.INC(Array;k)	Returns the k-th percentile of values in a range	Inputs linked to data X[1;2;3;4;5]): PERCENTILE.INC([X⇕];1) ⇒ 5
STDEV	STDEV(Number1;Number2; ... )	Estimates standard deviation based on a sample	Inputs linked to data X[1;2;3;4;5]): STDEV([X⇕]) ⇒ 1.581
STDEV.P	STDEV.P(Number1;Number2; ... )	Calculates standard deviation based on the entire population	Inputs linked to data X[1;2;3;4;5]): STDEV.P([X⇕]) ⇒ 1.414
STDEV.S	STDEV.S(Number1;Number2; ... )	Estimates standard deviation based on a sample	Inputs linked to data X[1;2;3;4;5]): STDEV.S([X⇕]) ⇒ 1.581
MODE	MODE(Number1;Number2; ... )	Returns the most common value in a data set	Inputs linked to data X[1;2;3;4;5]): MODE(([X⇕]) ⇒ NAN MODE(([X⇕];3) ⇒ 3
MEDIAN	MEDIAN(Number1;Number2; ... )	Returns the median of the given numbers	MEDIAN(1;2;3;4;5;6;7) ⇒ 4

Lookup

Name	Syntax, parameters	Description	Example
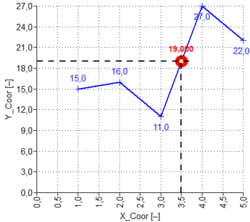
INDEX	INDEX(Array;Index)	Uses an index to choose a value from a reference or array	Inputs linked to data Y[15;16;11;27;22]): INDEX([Y⇓];2) ⇒ 16 INDEX([Y⇓];4) ⇒ 27 INDEX([Y⇓];9) ⇒ NAN
LINEARINTERPOLATION	LINEARINTERPOLATION(X;Coordinates X;Coordinates Y)	Calculates Y corresponding to X based upon linear interpolation of coordinates X, Y		Result of Linear Interpolation
MATCH	MATCH(Value;Array;[ Type = 1 ])	Looks up values in a reference or array - Type = 1 find max. value less or equal to Value ...values in Array must be sorted in ascending order - Type = -1 find min. value greater or equal to Value ...values in Array must be sorted in descending order - Type = 0 find first value equal to Value ...values in Array needn't to be sorted	Inputs linked to data Y[15;16;11;27;22]): MATCH(11;[Y⇕]) ⇒ 3 MATCH(27;[Y⇕]) ⇒ 4 MATCH(999;[Y⇕]) ⇒ NAN

Matrix

Name	Syntax, parameters	Description	Example
FILTERTABLE	FILTERTABLE(Coordinates X;Coordinates Y)	Filters repeating values and keeps the last one of them Returns matrix with 2 columns: Column 1: X - Filtered X Column 2: Y - Filtered Y
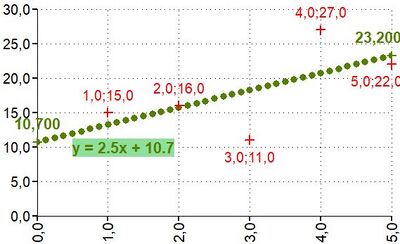
LINEARTREND	LINEARTREND(Coordinates X;Coordinates Y)	Returns the linear trend line Returns matrix with 1 row and 2 columns: Row Col. 1 Col. 2 1. k - Slope q - Offset	Inputs linked to data X[1;2;3;4;5]; Y[15;16;11;27;22] LINEARTREND([X⇕];[Y⇕]) NumRows = 1 Row Col. 1 Col. 2 1 2.5 10.7	Results of linear trend
LINEARTRENDANDPOINTS	LINEARTRENDANDPOINTS(Coordinates X;Coordinates Y)	Returns the linear trend line and its point representation Returns matrix with 2 rows and 4 columns: Row Col. 1 Col. 2 Col. 3 Col. 4 1. k - Slope q - Offset X1 Y1 2. NAN NAN X2 Y2	Inputs linked to data X[1;2;3;4;5]; Y[15;16;11;27;22] LINEARTREND([X⇕];[Y⇕]) NumRows = 2; Row Col. 1 Col. 2 Col. 3 Col. 4 1. 2.5 10.7 0 10.7 2. NAN NAN 5 23.2
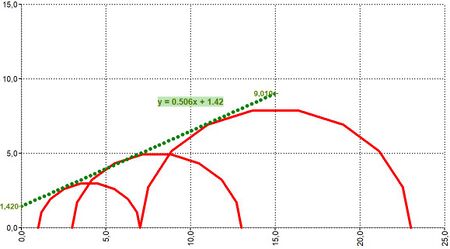
LINEARTRENDSC	LINEARTRENDSC(Center X;Radius)	Returns the linear trend line for semi-circles Returns matrix with 1 row and 2 columns: Row Col. 1 Col. 2 1. k - Slope q - Offset	Inputs linked to data X[4;8;15]; R[3;5;8] LINEARTRENDSC([X⇕];[R⇕]) NumRows = 1 Row Col. 1 Col. 2 1 0.506 1.42	Results of linear trend and points
LINEARTRENDSCANDPOINTS	LINEARTRENDSCANDPOINTS(Center X;Radius)	Returns the linear trend line for semi-circles and its point representation Returns matrix with 2 rows and 4 columns: Row Col. 1 Col. 2 Col. 3 Col. 4 1. k - Slope q - Offset X1 Y1 2. NAN NAN X2 Y2	Inputs linked to data X[4;8;15]; R[3;5;8] LINEARTRENDSCANDPOINTS([X⇕];[R⇕]) NumRows = 2 Row Col. 1 Col. 2 Col. 3 Col. 4 1. 0.506 1.42 0 1.42 2. NAN NAN 15 9.01
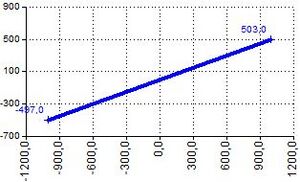
LINEARTRENDTOPOINTS	LINEARTRENDTOPOINTS(Slope;Offset)	Returns points of the linear trend line Returns matrix with 2 rows and 2 columns: Row Col. 1 Col. 2 1. X1 Y1 2. X2 Y2	LINEARTRENDTOPOINTS(0,5;3) NumRows = 2 Row Col. 1 Col. 2 1. -1000 -497 2. 1000 503	Results of linear trend
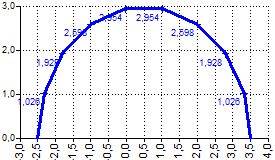
SEMICIRCLETOPOINTS	SEMICIRCLETOPOINTS(Center X;Radius;[Points count 10])	Returns points of the semi-circle Returns matrix with 2 rows and [Points count] columns: Row Col. 1 Col. 2 1. X1 Y1 2. X2 Y2 ... ... ... ... ... ... [Points count] Xn Yn	SEMICIRCLETOPOINTS(0,5;3;10) NumRows = 10 Row Col. 1 X Col. 2 Y 1. -2,5 0 2. -2,31908 1,02606 3. -1,79813 1,928363 4. -1 2,598076 5. -0,02094 2,954423 6. 1,020945 2,954423 7. 2 2,598076 8. 2,798133 1,928363 9. 3,319078 1,02606 10. 3,5 3,67E-16	Results of semi-circle to points
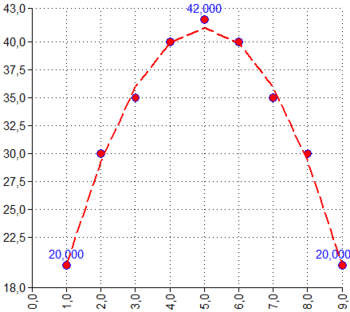
POLYNOMIALTREND	POLYNOMIALTREND(Coordinates X;Coordinates Y;[Order=2];[Force origin=False])	Returns the polynomial trend curve Returns matrix with 1 columns: Column 1 coefficients: c - Coefficients c0 + c1*x + c2*x2 + ...	POLYNOMIALTRENDANDPOINTS([X-Input⇕];[Y-Input⇕];2;9) Order = 2 Points count = 9 Coeff.: c0 = 8,238; c1 = 13.203; c2 = -1.32 Approx. formula: y = -1,32x2 + 13,203x + 8,238 Results: Row Col. 1 c Col. 2 X Col. 3 Y 1. 8.238 1 20.121 2. 13.203 2 29.364 3. -1.32 3 35.965 4. 4 39.926 5. 5 41.247 6. 6 39.926 7. 7 35.965 8. 8 29.364 9. 9 20.121	Results of PolynomialPoints approximation
POLYNOMIALTRENDANDPOINTS	POLYNOMIALTRENDANDPOINTS(Coordinates X;Coordinates Y;[Order=2 ];[Points count=10];[Force origin=False])	Returns the polynomial trend curve and its point representation Returns matrix with 3 columns: Column 1 coefficients: c - Coefficients c0 + c1*x + c2*x2 + ... Column 2: X - Coordinates X Column 3: Y - Coordinates Y Force origin: True ... if you want include point (0,0) in Coordinates X and Y
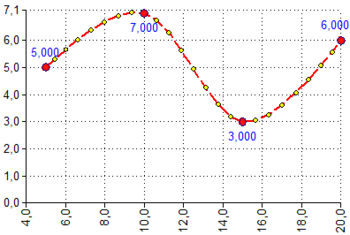
SPLINE	SPLINE(Coordinates X;Coordinates Y;[Points count=20])	Returns points of the spline running through given points Returns matrix with 2 columns: Column 1: X - Coordinates X Column 2: Y - Coordinates Y Coordinates X and Y are part of the Spline curve Inputs: Row X Y 1. 5 5 2. 10 7 3. 15 3 4. 20 6	SPLINE([X-Input⇕];[Y-Input⇕];[Num of Points]) Num of Points = 8 Results: Row Col. 1 X Col. 2 Y 1. 5,000 5,000 2. 5,465 5,313 3. 6,016 5,668 4. 6,633 6,035 5. 7,296 6,385 6. ... ...	Result of Spline function

Informative

Name	Syntax, parameters	Description	Example

Geotechnic

Name	Syntax, parameters	Description	Example